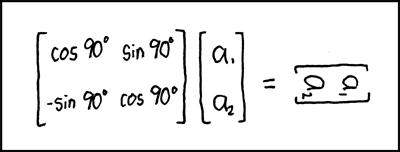CS184 Section 1
Introduction/Linear Algebra
Brandon Wang
January 24, 2012
Material adapted from Fu-Chung Huang, Ravi Ramamoorthi, and Carlo Sequin
Logistics/About Me
- brandonwang@berkeley.edu
- OH: W 2:30-3:30pm, Th 2-3pm in 651 Soda (6th Floor Alcove)
- HW0a due this week!
- These slides will be posted... somewhere
- (Yes, they are Google's HTML5 slides)
Today
- (Re) Introduction to Computer Graphics
- Review on Linear Algebra
Computer Graphics

Source: Disney/Pixar Toy Story 3
Computer Graphics

Computer Graphics

Source: Apple Mac OS X Lion
Other Applications
- CAD
- Simulation
- Fabrication
- Vision
- Art
- Happiness
- ...etc
Computer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware.
Computer graphics are programmed pretty pictures.
Our class
We're primarily focusing on the Computer Science part of
3D Computer Graphics.
For our assignments, we'll be using C++, OpenGL, and
GLSL.
What we learn can be extended to any language
(Python, Java, Scheme...), and we learn the underlying theory behind it all.
(So you can use DirectX later... If you really, really, really want to.)
Modeling
| Modeling |
Animation |
Rendering |
v -3.000000 1.800000 0.000000
v -2.991600 1.800000 -0.081000
v -2.991600 1.800000 0.081000
v -2.989450 1.666162 0.000000
...

Usually created by artists (UCBUGG), but can be scanned, math function (on an assignment)
Animation
| Modeling |
Animation |
Rendering |
(Sometimes optional)
...But usually artists. (UCBUGG)
Rendering
| Modeling |
Animation |
Rendering |




Source: CS184 Fu-Chung Huang
Linear Algebra: Vectors
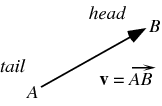
- Vectors encode length and direction.
- Use this to store offsets, displacements, "locations."
- Usually written as
\vec{a}
- Magnitude is usually written as
||a||
- We will (mostly) be using Cartesian Coordinates:
\vec{a} = x_a\vec{x} + y_a\vec{y} + z_a\vec{z}
\vec{a} = \left( \begin{matrix} x_a\\ y_a \end{matrix} \right)
\vec{a}^T = \left( \begin{matrix} x_a & y_a \end{matrix} \right)
||\vec{a}|| = \sqrt{x^2+y^2}
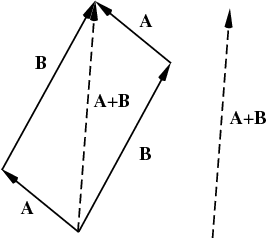
Linear Algebra: Vector Addition
Linear Algebra: Dot (Scalar) Product
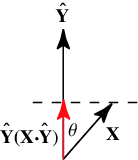
\vec{x}\cdot\vec{y} = ||x||\ ||y|| \cos{\theta}
\vec{a} \cdot (\vec{b}+\vec{c}) = a\cdot b + a \cdot c
(k\vec{a})\cdot \vec{b} = \vec{a}\cdot (k\vec{b}) = k(\vec{a}\cdot \vec{b})
Linear Algebra: Cross (Vector) Product
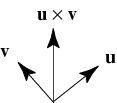
- Use the right-hand rule
\vec{a} \times \vec{b} = -\vec{b} \times \vec{a}
||\vec{u} \times \vec{v}|| = ||\vec{u}||\ ||\vec{v}||\ \sin{\phi}
- In 3D:
\vec{u}\times\vec{v} = (u_yv_z-u_zv_y)\vec{x}+(u_zv_x-u_xv_z)\vec{y}+(u_xv_y-u_yv_x)\vec{z}
Linear Algebra: Orthonormal Bases/Coordinate Frames
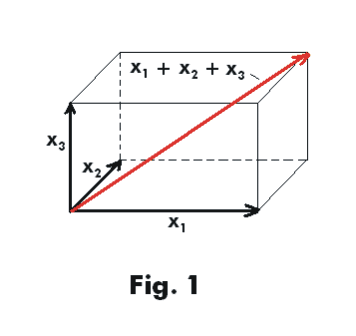
- In
\mathbb{R}^n
: Set of n real-valied orthonormal vectors
- Any vector in
\mathbb{R}^n
can be represented by a linear combination of these vectors
- In
\mathbb{R}^3
(3D), we commonly refer to them as x, y, z.
Linear Algebra: Matrices
\left( \begin{matrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{matrix} \right)
Linear Algebra: Matrix Multiplication
(AB)_{i,j} = \sum_{k=1}^p A_{ik}B_{kj}
A=\begin{bmatrix}a&b\\c&d\end{bmatrix}
, B=\begin{bmatrix}e&f\\g&h\end{bmatrix}
AB=\begin{bmatrix}a&b\\c&d\end{bmatrix}\begin{bmatrix}e&f\\g&h\end{bmatrix}=\begin{bmatrix}ae+bg&af+bh\\ce+dg&cf+dh\end{bmatrix}
Linear Algebra: Matrix Transpose
\begin{bmatrix}
1 & 2 \end{bmatrix}^{\mathrm{T}} \!\! \;\!
= \,
\begin{bmatrix}
1 \\
2 \end{bmatrix}.
\begin{bmatrix}
1 & 2 \\
3 & 4 \end{bmatrix}^{\mathrm{T}} \!\! \;\!
= \,
\begin{bmatrix}
1 & 3 \\
2 & 4 \end{bmatrix}.
\begin{bmatrix}
1 & 2 \\
3 & 4 \\
5 & 6 \end{bmatrix}^{\mathrm{T}} \!\! \;\!
= \,
\begin{bmatrix}
1 & 3 & 5\\
2 & 4 & 6 \end{bmatrix}. \;
Linear Algebra: Identity Matrix
I_1 = \begin{bmatrix}
1 \end{bmatrix}
,\
I_2 = \begin{bmatrix}
1 & 0 \\
0 & 1 \end{bmatrix}
,\
I_3 = \begin{bmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1 \end{bmatrix}
,\ \cdots ,\
I_n = \begin{bmatrix}
1 & 0 & \cdots & 0 \\
0 & 1 & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & 1 \end{bmatrix}
Linear Algebra: Transformations
Linear Algebra: Transformations
Think about it this way:
(Credit to XKCD and Brian Maissy for posting it on Piazza)
Linear Algebra: Questions
1. Find the length of vector
\vec{x} = \left( \begin{matrix} 3\\-6\\2 \end{matrix} \right)
||\vec{x}|| = \sqrt{3^2+(-6)^2+2^2} = 7
2.
What is
\vec{x}\times\vec{z}
Linear Algebra: Questions
Given two
\mathbb{R}^2
vectors, \vec{i}
and \vec{j}
, \vec{i}\cdot\vec{i}=1, \vec{i}\cdot\vec{j}=0, \vec{j}\cdot\vec{j}=1
- Does a vector
\vec{k}
exist, such that \vec{k}\neq\vec{i}
, \vec{k}\cdot\vec{k}=1
, \vec{k}\cdot\vec{j}=0
? What is it? How many are there?
- Does a vector
\vec{k}
exist, such that \vec{k}\cdot\vec{i}=0
, \vec{k}\cdot\vec{k}=1
, \vec{k}\cdot\vec{j}=0
? What is it? How many are there?
- Do the answers change if
\vec{i}
and \vec{j}
are in \mathbb{R}^3
?
Linear Algebra: Questions
Given
p_1, p_2, p_3 \in \mathbb{R}^2
vectors, consider the cross product
n = (p_2-p_1)\times(p_3-p_1)
What does this vector mean geometrically?
Let
p
be any point in the plane containing p_1,p_2,p_3
. What is the geometric relationship between p-p_1
and n
(look at their dot product)?
Linear Algebra: Questions
Write the parametric equation for a line through points p1 and p2. Now write
the parametric equation for a plane through points p1, p2, and p3.
Show
how to restrict these parametric equations to specify only the points on the
line segment between p1 and p2 for the line, and only the points inside the
triangle formed by p1, p2, and p3 for the plane.
Thanks!
- Rendering pictures by Fu-Chung Huang
- Math review adapted from Ravi Ramamoorthi's slides and Wikipedia
- HTML5 slides from Google
- Questions from Carlo Sequin