CS184 Section 11
Brandon Wang
Logistics
Today
Acceleration Structures
Hopefully you have the intuition behind ray tracing now. You shoot rays from
the camera, and find what intersects the ray.
Last time, we looped through every primitive (triangle, etc) to see if they
intersected. This is very slow!
Radiosity
Why we care
Radiometry - What are we trying to describe?
Okay so, we've been shooting rays and computing color values.
But what is the mathematical formalization behind this, and can we describe
real scenes?
Our goal is to tie together the brightness and energy bouncing around the scene
and eventually hitting our eyes
This ends up with a lot of Physics-like things, and complicated terms. Hopefully, this will help you organize them...
Radiosity - Terms
BRDF
The bidirectional reflectance distribution function
sr^{-1}
L is radiance, E is irradiance,
\theta_i
is the angle made between \omega_i
and surface normal n
f_r(\omega_i, \omega_o)=\frac{dL_r(\omega_o)}{dE_i(\omega_i)}=\frac{dL_r(\omega_o)}{L_i(\omega_i)\cos\theta_i\,d\omega_i}
wat
BRDF
The bidirectional reflectance distribution function
How light is reflected at an opaque surface. Takes in the incoming light in
\omega_i
and outgoing light in \omega_o
, and gives you the ratio of the radiance exiting along
\omega_o
to the irradiance incident on the surface from direction \omega_i
BRDF
Wait that picture looks familiar
We defined shading in HW2,3,5(,6) using pictures like these, and we said that it was a combination of lambertian and specular terms.
You have already implemented two BRDFs: the Lambertian model, and the Blinn-Phong model.
Other BRDFs include the Torrance-Sparrow model (accounting for microfacets in specular highlights), Oren-Nayar (accounting for microfacets in diffuse surfaces), and various anisotropic models
Rendering Equation
L_o(\mathbf x, \omega) = L_e(\mathbf x, \omega) + \int_\Omega f_r(\mathbf x, \omega', \omega) L_i(\mathbf x, \omega') (-\omega' \cdot \mathbf n) d \omega'
L_o(\mathbf x, \omega)
is the total amount of light directed outward along direction \omega
, from a particular position \mathbf x\,\!
L_e(\mathbf x, \omega)
is emitted light\int_\Omega \cdots d\omega'
is an integral over a hemisphere of inward directionsf_r(\mathbf x, \omega', \omega)
is the BRDF, the proportion of light reflected from \omega'
to \omega
at position \mathbf x\,\!
L_i(\mathbf x, \omega')
is light coming inward toward \dmathbf x\,\!
from direction \omega'
at time t\,\!
-\omega' \cdot \mathbf n
is the attenuation of inward light due to incident angle
Rendering Equation (with wavelength and time)
L_o(\mathbf x, \omega, \lambda, t) = L_e(\mathbf x, \omega, \lambda, t) + \int_\Omega f_r(\mathbf x, \omega', \omega, \lambda, t) L_i(\mathbf x, \omega', \lambda, t) (-\omega' \cdot \mathbf n) d \omega'
\lambda\,\!
is a particular wavelength of lightt\,\!
is timeL_o(\mathbf x, \omega, \lambda, t)
is the total amount of light of wavelength \lambda\,\!
directed outward along direction \omega
at time t\,\!
, from a particular position \mathbf x\,\!
L_e(\mathbf x, \omega, \lambda, t)
is emitted light\int_\Omega \cdots d\omega'
is an integral over a hemisphere of inward directionsf_r(\mathbf x, \omega', \omega, \lambda, t)
is the BRDF, the proportion of light reflected from \omega'
to \omega
at position \mathbf x\,\!
, time t\,\!
, and at wavelength \lambda\,\!
L_i(\mathbf x, \omega', \lambda, t)
is light of wavelength \lambda\,\!
coming inward toward \mathbf x\,\!
from direction \omega'
at time t\,\!
-\omega' \cdot \mathbf n
is the attenuation of inward light due to incident angle
Time?
VIDEO
Conceptual Questions
From a perfectly lambertian/diffuse surface, is there an equal amount of energy radiated in different directions?
No, foreshortened area falls off as cos.
Is there an equal amount of radiance in different directions?
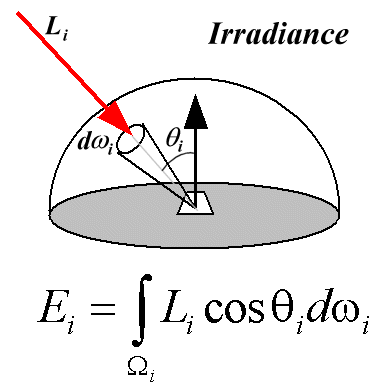
Relating Radiance and Irradiance
Radiance (L) - Power traveling at some point in a specified direction per foreshorteded area per unit solid angle.
W \cdot m^{-2} \cdot sr^{-1}
Irradiance (E) - Total power per unit area coming into or leaving a location on the surface.
W \cdot m^{-2}
E(x) = \int_{H^2}L_i(x,\omega)\cos\theta d\omega
So what does this formalism get us?
We actually get quite a few nice things...
Light fields
5 or 4 dimensional function of amount of light.
x,y,z,\theta\,\phi
Basis of the Lytro camera
Rendering Stuff Accurately
Making stuff
(video)
Tips for the final
Review your midterm. Remember that the final is cumulative!
Remember that not all topics covered were done in projects.
Review.